Idea 055 - Truchet tessellating bathroom tiles

This post is part of the 100 project ideas project. #The100DayProject. I am looking for feedback. Comment below or DM me via social media Instagram, Twitter.

One Line Pitch

Elevate your bathroom or kitchen with unique and meaningful ceramic tiles inspired by mathematical shapes and designs that are both visually stunning and tell a story

Description

Most bathroom, or kitchen back splash tiles are boring periodic tiling of squares, rectangles, and maybe if you are lucky hexagonal (aka the Bestagons.) tiles. Same repeating Tessellating geometric shapes with no overlap or gaps. Because of the regular shape it’s easy to install over an arbitrary size wall, and contractors love “easy”.

There are many other geometric shapes, and tiling patterns that are much more interesting. Some of them are easy to install but still visually interesting.

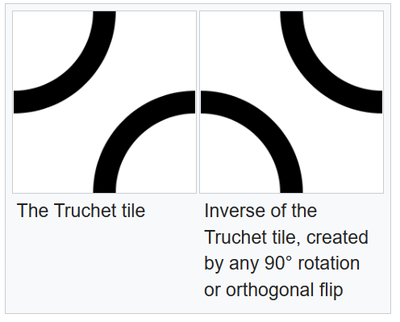
Truchet tiles are square tiles decorated with patterns that are not rotationally symmetric. When placed in a square tiling of the plane, they can form varied patterns, and the orientation of each tile can be used to visualize information associated with the tile’s position within the tiling.

A common version of the truchet tiles are Quarter-circles. A single tile with two quarter-circles connecting the midpoints of adjacent sides.

If you randomly place this tile on the wall it will create interesting patterns. It’s a square tile and should be easy as the existing tiles to install but much more interesting and has a story behind it. I have made laser cut wood versions of this kind of tiling for art projects.

Aperiodic tiling - is a non-periodic tiling with the additional property that it does not contain arbitrarily large periodic regions or patches. The Penrose tilings are a well-known example of aperiodic tilings.

A common example of Aperiodic tiling is Penrose tiling. This can tile a plane (the wall) with a non repeating for an infinity distance. No matter how you place them on the wall you will not get a repeating pattern. Penrose tilings may have both reflection symmetry and fivefold rotational symmetry.

The Infinite Pattern That Never Repeats by Veritasium is a great video that goes into detail about how amazing Penrose tiling is.

Consisting of a Kite and dart tiles it is more complex for installation on a bathroom wall but it’s much more interesting with a great back story.

Examples of Penrose tiling in the real world.

• Penrose tiles in Helsinki, related Penrose’s aperiodic tilings
• The foyer of the Mitchell Institute for Fundamental Physics and Astronomy - Roger Penrose standing on a floor with a Penrose tiling
• Three mathematical bathroom floors

There are many other examples of different tiling that would be more interesting than the normal tiles used for kitchen backsplash and bathroom tiling. Here are a few more examples

• Monnier Trapezium and Diamond - uses a trapezium and a rhomb
• Ammann-Beenker - Aperiodic tiles, 8 fold symmetry
• Danzer’s 7-fold original - 14-fold symmetry
• Semi-detached House - Weird and interesting.
• Wanderer (rotations) - Simple square rotation.
• Quartic pinwheel - Complex but interseting.
• More - A whole bunch of other interesting tiling shapes

Inspiration for this post came from this hackernews post Mathematicians discover shape that can tile a wall and never repeat

The idea is to create these ceramic tiles for bathroom and kitchen backsplashes.

The potential pitfalls to consider when it comes to the installation process. The more complex the tile design, the more difficult it may be for contractors to install them, which could result in higher costs and longer installation times. Additionally, the market may be limited to those who are interested in unique and mathematically-inspired designs.

Prior art and links

• Tilings Encyclopedia - The tilings encyclopedia shows a wealth of examples of nonperiodic substitution tilings.
• Wang tile - are modeled visually by square tiles with a color on each side. A set of such tiles is selected, and copies of the tiles are arranged side by side with matching colors, without rotating or reflecting them.
• Serpentiles - Serpentiles is the name coined by Kurt N. Van Ness for the hexagonal tiles used in various edge-matching puzzle connection abstract strategy games
• StampID - “stampID” is a set of procedurally generated stamps. They follow the rule of truchet tiles: each tile edge interfaces with the other edges. This way the stamp can be rearranged in multiple different ways to create new patterns. Each stamp set contains 3 stamps who have one, two and three interfacing sides. The stamp pattern itself is inspired by art nouveau swirls and celtic knots.

Market

The market for these unique and visually interesting tiling patterns for bathroom and kitchen backsplashes could be broad, encompassing homeowners, interior designers, architects, contractors, and anyone looking to add a creative and unique touch to their home or commercial space. The market could also potentially include those interested in art and mathematics, as the designs are inspired by geometric tiling patterns with fascinating mathematical properties. The appeal may be particularly strong for those who want to stand out from the typical square and rectangular tile patterns commonly used in bathrooms and kitchens.